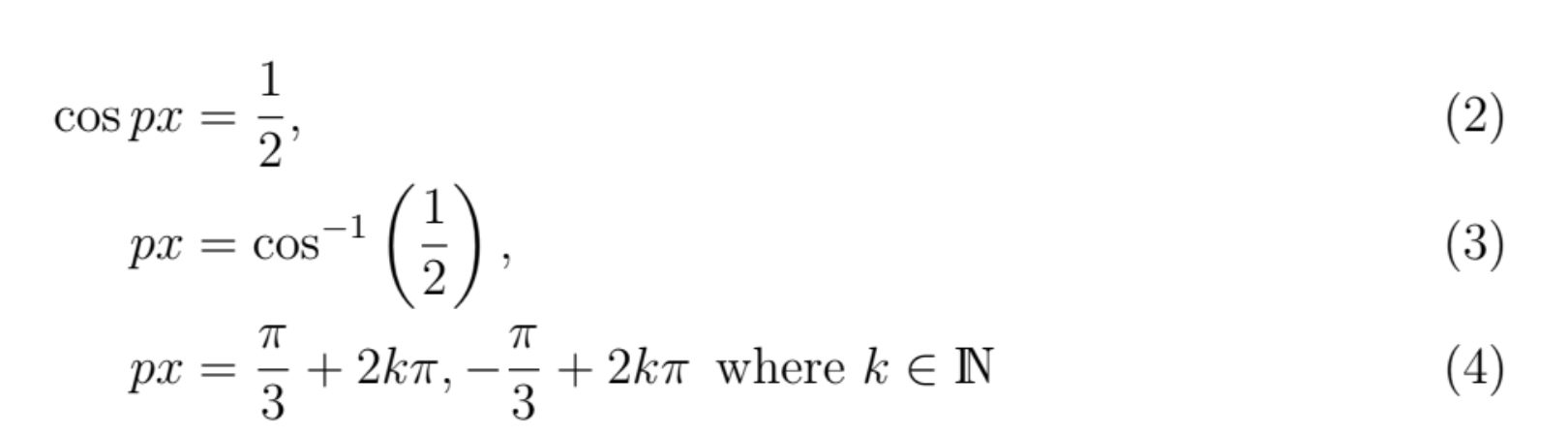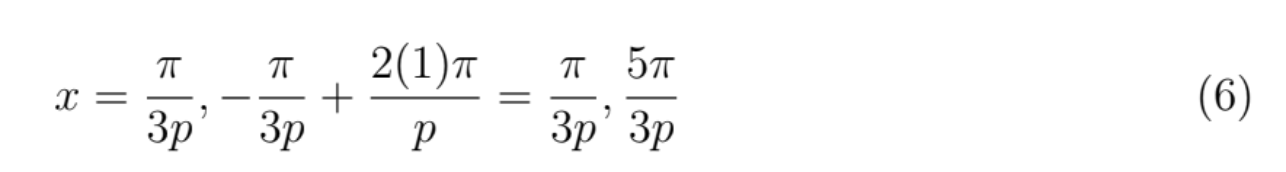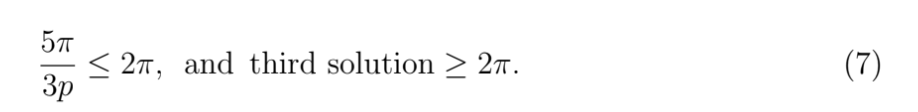Q32 of the 2025 Maths Advanced HSC
This year’s HSC Mathematics Advanced paper has left many students talking — and for good reason. It was arguably one of the most challenging Advanced papers in recent memory. Rather than relying solely on textbook-style applications of formulas, the exam demanded a deeper level of conceptual understanding, abstract reasoning, and strategic problem-solving.
The last question, Question 32 was no exception, requiring HSC candidates to blend algebraic manipulation, graphical reasoning, and logical deduction to achieve full marks for the question.
Let’s examine how this question could be solved, and the theory behind it!
1) Understanding What The Question Is Asking
Question 31 asked students to find all possible values of a constant p, where,
cos px = 1/2 (1)
We are also told that this expression only has two solutions, where 0 ≤ x ≤ 2π and p > 0.
2) Graphical interpretation
Being able to understand HSC questions graphically is an extremely important skill for all high school levels of math, especially as the math starts to become more complex and demanding, seeing things graphically rather than purely equations on paper can make the process simpler.
If we graph what the function cos px looks like generally we find this,
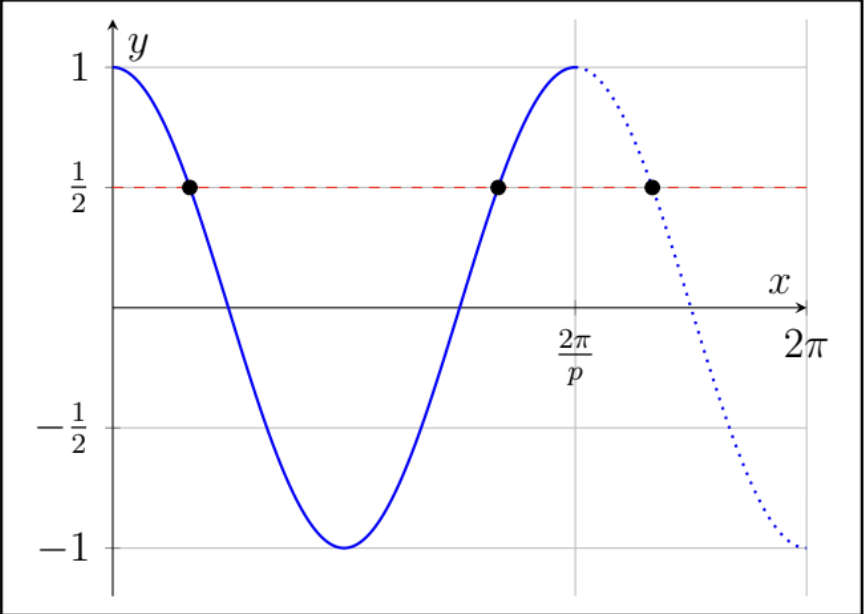
Figure 1: Graph of y = cos(px), boxed, with dashed line at y = 1/ 2 and marked intercepts.
Let’s consider the graph of y=cos(px) = \cos(px)y=cos(px):
As ppp increases, the graph compresses horizontally.
The line y=1/2 cuts through the cosine curve at points where the equation holds.
Looking at this graph, it is still a bit confusing as to what we should do next, so, when stuck, the best next step would be to attempt to move to an algebraic solution and solve the original equation cos px = 1/2, where the solutions will be the points of interception in Figure 1.
3) Solving the Equation
To solve the given equation for x to find the points of interception, we will follow the standard procedure as shown below.
We express the solutions as px = π/3 + 2kπ, −π/3 + 2kπ with k as an element of naturalvnumbers (i.e. 1, 2, 3, 4, 5, .... the solutions px =π/3, −vπ/3vhave a period of 2π, meaning all solutions can simply be expressed as π/3 or − π/ 3 multiplied by a positive whole number, in this case k. Thus in order to find the full range of solutions for x, we will divide the equation in (4) by p, giving the following rule,
Because we are told in the question that the solutions for x are 0 ≤ x ≤ 2π, and because p > 0, we know for a fact that x =/ − π/3p , as p > 0 means that this will be a negative solution, not satisfying the requirements. Because we also know that there are only two solutions within the domain 0 ≤ x ≤ 2π, the only possible solutions that we can have for
Thus, if we label the solutions we have found in (6) into Figure 1, such that the cos px = 1/2 only has two solutions, we can represent it as:
Now that we have found the only possible solutions for the equation cos px = 1/2, we can sketch a far more accurate graph of what the solutions will look like, as they satisfy the conditions that there are only two solutions which exist in 0 ≤ x ≤ 2π.
4) Finding an Inequality
Going back to the start of the question, students are asked to find all possible values of some constant p. This is a pretty daunting thing to ask, as it is unclear what is meant by ’all possible values’. However, one trick that is super handy to know when sitting the HSC, is that an ’all possible values’ question typically equates to a ’find an inequality’ question. So we need to find some inequality that describes p in order to satisfy the conditions given.
Looking at Figure 2, we can see that for any value of p, that in order to satisfy the condition that only two solutions are present in 0 ≤ x ≤ 2π, the second solution must be less than 2π, and the third solution must be greater than 2π. If we go about expressing this mathematically and using the value for the second solution found in (6), we find that,
Lets first solve the first inequality found in (7) using standard methods:
Great! Now that we have obtained the first part of the solution p ≥ 5/6, lets solve the inequality for the third solution being greater than or equal to 2π. Using the general rule for solutions set up in (5), we can simply say that the third solution is,
Which represents the third dot in Figure 2. Now all we need to do as shown in Figure 2 and (7), is find the values of p such that,
Expanding this out,
Thus, because p has to satisfy both of the conditions found in (11) and (16), we can simply combine them, giving us the answer and final range of solutions for p. i.e.
4) Final thoughts and tips
This years last question certainly required a higher level of abstract thinking which is somewhat unfair of NESA to ask stressed students to complete in exam conditions, and as shown above it is fairly involved. However, because it is unfortunately the case that as a student you must prepare for anything NESA can throw your way, here are some general tips that help going about Trig equations, as well as abstract thinking problems:
Use graphs and visual representations for ANY problem solving question as they make them less abstract and more grounded,
Using the ’+2kπ’ trick from (4) helps save time rather than trialing and error different values to find solutions
If a question says ”all possible values”, aim to find some sort of inequality,
Ensure that the initial conditions in these problem solving questions are crystal clear and a you understand exactly what they mean and how they might effect the question (e.g, only two solutions in the given domain),
Learning exact values for trig functions saves lots of time and builds confidence rather than relying on a calculator,
Regular practice with these question builds a level of intuition and problem solv- ing which makes a band 6 more obtainable (as obvious as that sounds it is entirely true!!)
If you’re aiming to strengthen your understanding of HSC Mathematics or want guidance on mastering challenging problems like this, reach out to Pinnacle Learners. Offering both online and in-person tutoring from our office in Rozelle, yur expert tutors specialise in building the conceptual depth, confidence, and exam skills you need to reach your mathematical potential.
Contact Pinnacle Learners today and take the next step toward your best HSC results!